And solitaire’s the only game in town (Neil Sedaka, 1974)

Antes del Kinect y del WII, antes del GameBoy o del Tetris, antes incluso del Pong; los niños se entretenían en sus vacaciones –cuando no estaban haciendo “playitas” en el mar o tratando de ganarse un tarro de duraznos en la lotería– con juegos de cartas o de mesa: reinaban el Ludo, las Damas y el Tablero Chino, todos juegos de competencia en que había que desplazar fichas a través de casilleros. Si no se tenían hermanos y los papás no querían jugar con uno, quedaba siempre al fondo de la caja de los esparcimientos veraniegos un solitario tablero que se denominaba, justamente, solitario; un rompecabezas en forma de cruz de 32 fichas (en inglés, pegs) y 33 espacios (el central vacío) cuyo objetivo consistía en dejar solamente una ficha al medio, cómo se muestra en el siguiente dibujo (posiciones inicial y final).

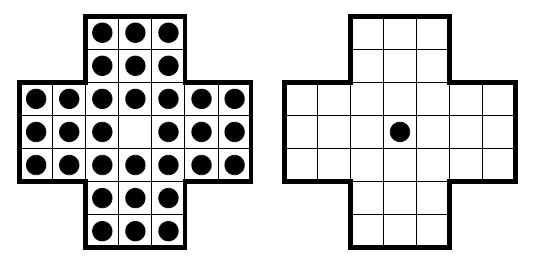La regla del juego era única: solo se podía mover una ficha a la vez saltando otra (solo una) hacia un espacio vacío, y tras el salto se eliminaba la ficha que había sido saltada (tal como en las damas).

Recuerdo especialmente un verano en que no tenía ganas de ir a la playa que pasé obsesionado con encontrar una solución. A veces me quedaban dos fichas separadas; en mis mejores tardes dejaba una, pero no en el centro. Estaba entrando a desesperarme. Sospechaba que no había manera de ganar. Entonces un tío se me acercó y me dio la iluminación topológica de mi infantoadolescencia: “¿te has fijado en que el juego es simétrico?”. “¿Cómo es eso?”. “Mira, el juego parte con un espacio al centro, y termina con una ficha al centro. Eso significa que el juego puede jugarse al revés: partir con una ficha al medio, saltar un espacio y dejar una ficha en la posición saltada, y así, hasta llenar el tablero, dejando un espacio al medio”.

La genial idea de mi tío me envalentonó: primero traté de jugarlo a la inversa, pero, era igualmente difícil que en el sentido habitual. Luego me percaté de lo que había que hacer: buscar una posición a la que pudiera llegar tanto desde el sentido directo del juego, como desde el sentido inverso. Si encontraba esa posición, estaría resuelto. Y así ocurrió. Encontré una de esas posiciones.

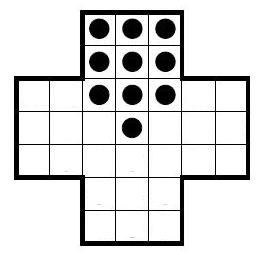Luego la cosa fue sencilla: me aprendí de memoria los pasos para llegar a esa posición tanto en sentido habitual como inverso; y me cachiporreé de lo lindo el resto del verano.

Puede hacer su propia prueba de este método y buscar sus nuevas respuestas: según un artículo en arXiv de George Bell (2011) hay 40.861.647.040.079.968 maneras de ganar. De hecho, en el mismo artículo y en otros compilados por el mismo autor en su precioso sitio: Peg Solitaire, se llama a este tipo de aproximación el modelo “complementario”.

Si no se anima a buscar su propio sistema (porque prefiere las “playitas” y los tarros de duraznos), acá un gráfico de una de las formas de vencer.

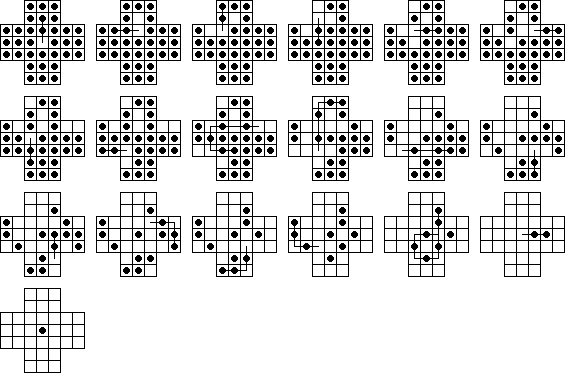Y una cancioncita: